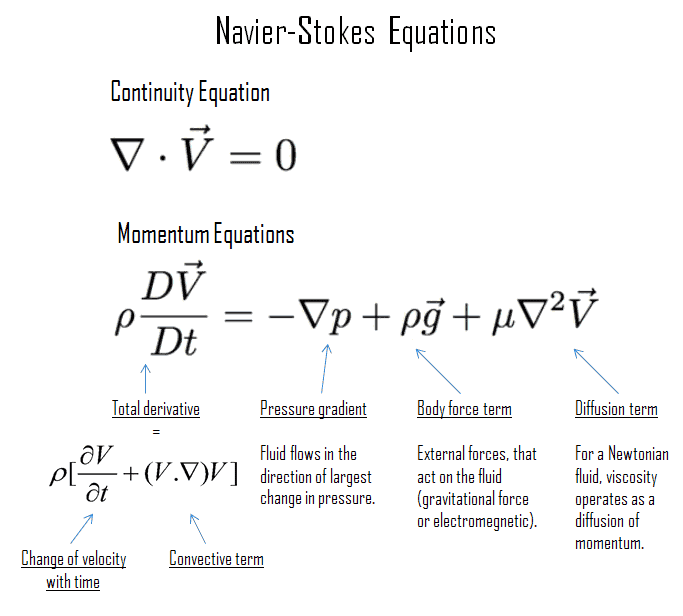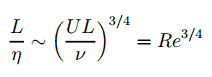Equations de Navier-Stokes
En dynamique des fluides , les équations de Navier-Stokes sont des équations décrivant le mouvement tridimensionnel de substances fluides visqueuses . Ces équations sont nommées d’après Claude-Louis Navier (1785-1836) et George Gabriel Stokes (1819-1903). Dans les situations où il n’y a pas de forts gradients de température dans le fluide, ces équations fournissent une très bonne approximation de la réalité .
Les équations de Navier-Stokes consistent en une équation de continuité dépendant du temps pour la conservation de la masse , trois équations de conservation dépendantes du temps et une équation de conservation de l’énergie dépendantes du temps. Il y a quatre variables indépendantes dans le problème, les coordonnées spatiales x, y et z d’un domaine et le temps t.
Comme on peut le constater, les équations de Navier-Stokes sont des équations aux dérivées partielles non linéaires du second ordre; leurs solutions ont été trouvées pour résoudre divers problèmes intéressants d’écoulement visqueux. Ils peuvent être utilisés pour modéliser les conditions météorologiques, les courants océaniques, le flux d’air autour d’une surface portante et le flux d’eau dans une conduite ou un réacteur. Les équations de Navier – Stokes sous leur forme complète et simplifiée aident à la conception des avions et des voitures, à l’étude du flux sanguin, à la conception des réacteurs nucléaires et à bien d’autres choses.
Solution des équations de Navier-Stokes
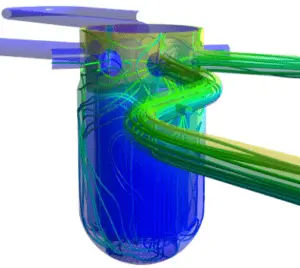
Source: groupe de développement CFD – hzdr.de
Même si les équations de Navier-Stokes ne contiennent qu’un nombre limité de solutions analytiques connues, elles peuvent être modélisées par ordinateur. Le principal outil disponible pour leur analyse est l’ analyse CFD . CFD est une branche de la mécanique des fluides qui utilise l’analyse numérique et des algorithmes pour résoudre et analyser des problèmes impliquant des écoulements de fluide turbulent. Il est largement admis que les équations de Navier – Stokes (ou les équations simplifiées de Navier – Stokes à la moyenne de Reynolds ) sont capables de présenter des solutions turbulentes, et ces équations sont à la base de pratiquement tous les codes CFD. Il est maintenant possible d’obtenir des résultats CFD approximatifs mais réalistes pour une grande variété d’écoulements visqueux complexes à deux et trois dimensions.
Les équations de Navier – Stokes présentent également un grand intérêt au sens purement mathématique. Malheureusement, le caractère hautement intermittent et irrégulier de l’ écoulement turbulent complique toutes les analyses . Il n’a pas encore été prouvé que les solutions en trois dimensions existent toujours, ou que si elles existent, elles sont lisses. En fait, la solution générale des équations de Navier-Stokes avec turbulences est souvent qualifiée de «dernier problème non résolu en physique mathématique classique».
Caractéristiques du flux turbulent
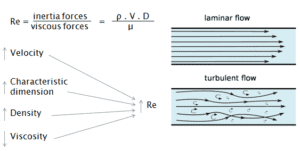Un écoulement turbulent a tendance à se produire à des vitesses plus élevées , à une faible viscosité et à des dimensions linéaires caractéristiques plus élevées .- Si le nombre de Reynolds est supérieur à Re> 3500, l’écoulement est turbulent.
- Irrégularité: L’écoulement est caractérisé par le mouvement irrégulier des particules du fluide. Le mouvement des particules fluides est chaotique. Pour cette raison, l’écoulement turbulent est normalement traité statistiquement plutôt que de manière déterministe.
- Diffusivité: Dans un écoulement turbulent, une distribution de vitesse assez plate existe à travers la section du tuyau, avec pour résultat que le fluide entier s’écoule à une valeur unique donnée et tombe rapidement extrêmement près des parois. La caractéristique qui est responsable du mélange amélioré et des taux accrus de transports de masse, de quantité de mouvement et d’énergie dans un flux est appelée «diffusivité».
- Rotationalité: l’ écoulement turbulent est caractérisé par un puissant mécanisme de génération de vortex tridimensionnel. Ce mécanisme est connu sous le nom d’étirement vortex.
- Dissipation: Un processus dissipatif est un processus dans lequel l’énergie cinétique de l’écoulement turbulent est transformée en énergie interne par une contrainte de cisaillement visqueuse.
Microscales Kolmogorov
De l’avis de Kolmogorov ( Andrey Nikolaevich Kolmogorov était un mathématicien russe qui a apporté une contribution significative aux mathématiques de la théorie des probabilités et de la turbulence), les mouvements turbulents impliquent une large gamme d’échelles . D’une échelle macroscopique à laquelle l’énergie est fournie, à une échelle microscopique à laquelle l’énergie est dissipée par la viscosité.
Par exemple, considérons un nuage cumulus. L’ échelle macroscopique du nuage peut être de l’ordre de kilomètres et peut croître ou persister sur de longues périodes. Dans le nuage, des tourbillons peuvent se produire sur des échelles de l’ordre du millimètre . Pour des débits plus petits tels que dans les tuyaux, les micro-échelles peuvent être beaucoup plus petites. La majeure partie de l’énergie cinétique de l’ écoulement turbulent est contenue dans les structures à grande échelle. L’énergie «passe en cascade» de ces structures à l’échelle macroscopique aux structures à l’échelle microscopique par un mécanisme inertiel. Ce processus est connu sous le nom de cascade d’énergie turbulente .
Les plus petites échelles de l’écoulement turbulent sont connues sous le nom d’ échelles de Kolmogorov . Celles-ci sont suffisamment petites pour que la diffusion moléculaire devienne importante et qu’une dissipation visqueuse de l’énergie ait lieu et que l’énergie cinétique turbulente soit dissipée en chaleur.
Les plus petites échelles en écoulement turbulent, c’est-à-dire les micro- échelles de Kolmogorov sont:
où ε est le taux moyen de dissipation de l’énergie cinétique de turbulence par unité de masse et a des dimensions (m 2 / s 3 ). ν est la viscosité cinématique du fluide et a des dimensions (m 2 / s).
La taille du plus petit tourbillon dans l’écoulement est déterminée par la viscosité. L’ échelle de longueur de Kolmogorov diminue à mesure que la viscosité diminue. Pour les flux à nombre de Reynolds très élevé , les forces visqueuses sont plus faibles par rapport aux forces inertielles. Des mouvements à plus petite échelle sont alors nécessairement générés jusqu’à ce que les effets de la viscosité deviennent importants et que l’énergie soit dissipée. Le rapport des échelles de longueur les plus grandes aux plus petites dans l’écoulement turbulent est proportionnel au nombre de Reynolds (augmente avec la puissance des trois quarts ).
Cela rend pratiquement impossible la simulation numérique directe d’un écoulement turbulent. Par exemple, considérons un flux avec un nombre de Reynolds de 10 6 . Dans ce cas, le rapport L / l est proportionnel à 10 18/4 . Comme nous devons analyser un problème tridimensionnel, nous devons calculer une grille qui comprenait au moins 10 14 points de grille . Cela dépasse de loin la capacité et les possibilités des ordinateurs existants.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci
