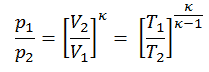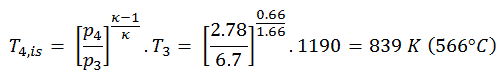Proceso isentrópico
Un proceso isentrópico es un proceso termodinámico , en el cual la entropíadel fluido o gas permanece constante. Significa que el proceso isentrópico es un caso especial de un proceso adiabático en el que no hay transferencia de calor o materia. Es un proceso adiabático reversible . Un proceso isentrópico también se puede llamar un proceso de entropía constante. En ingeniería, un proceso tan idealizado es muy útil para la comparación con procesos reales.
Dado que hay cambios en la energía interna (dU) y cambios en el volumen del sistema (∆V), los ingenieros a menudo usan la entalpía del sistema, que se define como:
H = U + pV
En muchos análisis termodinámicos es conveniente utilizar la entalpía en lugar de la energía interna. Especialmente en el caso de la primera ley de la termodinámica.
Proceso isentrópico y la primera ley
La primera ley de la termodinámica en términos de entalpía :
dH = dQ + Vdp
o
dH = TdS + Vdp

Ver también: Primera ley de la termodinámica.
Ver también: Ley del gas ideal
Ver también: Qué es la entalpía
dH = Vdp → W = H 2 – H 1 → H 2 – H 1 = C p (T 2 – T 1 ) (para gas ideal )
Expansión isentrópica – Compresión isentrópica
Ver también: ¿Qué es un gas ideal?
En un gas ideal , las moléculas no tienen volumen y no interactúan. Según la ley de los gases ideales , la presión varía linealmente con la temperatura y la cantidad, e inversamente con el volumen .
pV = nRT
dónde:
- p es la presión absoluta del gas
- n es la cantidad de sustancia
- T es la temperatura absoluta
- V es el volumen
- R es la constante de gas ideal, o universal, igual al producto de la constante de Boltzmann y la constante de Avogadro,
En esta ecuación, el símbolo R es una constante llamada constante de gas universal que tiene el mismo valor para todos los gases, es decir, R = 8.31 J / mol K.
El proceso isentrópico (un caso especial de proceso adiabático) se puede expresar con la ley de los gases ideales como:
pV κ = constante
o
p 1 V 1 κ = p 2 V 2 κ
en el que κ = c p / c v es la relación de los calores específicos (o capacidades de calor ) para el gas. Uno para presión constante (c p ) y otro para volumen constante (c v ) . Tenga en cuenta que esta relación κ = c p / c v es un factor para determinar la velocidad del sonido en un gas y otros procesos adiabáticos.
Otra relación p, V, T
En un diagrama pV , el proceso ocurre a lo largo de una línea (llamada adiabat ) que tiene la ecuación p = constante / V κ . Para un proceso ideal de gas y politrópico, el caso n = κ corresponde a un proceso isoentrópico.
Ejemplo: expansión isentrópica en turbina de gas
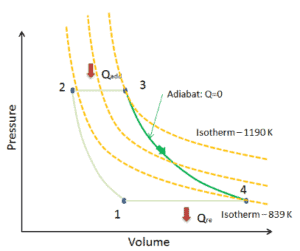
Suponga una expansión isentrópica de helio ( 3 → 4 ) en una turbina de gas . Como el helio se comporta casi como un gas ideal , use la ley del gas ideal para calcular la temperatura de salida del gas ( T 4, es ). En estas turbinas, la etapa de alta presión recibe gas (punto 3 en la figura; p 3 = 6.7 MPa ; T 3 = 1190 K (917 ° C)) de un intercambiador de calor y lo expulsa a otro intercambiador de calor, donde la presión de salida es p 4 = 2.78 MPa (punto 4) .
Solución:
La temperatura de salida del gas, T 4, se puede calcular utilizando p, V, T Relación para el proceso isentrópico (proceso adiabático reversible):
En esta ecuación, el factor para helio es igual a κ = c p / c v = 1.66 . De la ecuación anterior se deduce que la temperatura de salida del gas, T 4 , es:
Ejemplo: expansión isentrópica en turbina de gas

Supongamos el ciclo Brayton ideal que describe el funcionamiento de un motor de calor a presión constante . Los modernos motores de turbina de gas y los motores de inyección de aire también siguen el ciclo de Brayton.
El ciclo ideal de Brayton consiste en cuatro procesos termodinámicos. Dos procesos isentrópicos y dos procesos isobáricos.
- Compresión isentrópica : el aire ambiente ingresa al compresor, donde se presuriza (1 → 2). El trabajo requerido para el compresor viene dado por W C = H 2 – H 1 .
- adición de calor isobárico : el aire comprimido pasa a través de una cámara de combustión, donde se quema el combustible y se calienta el aire u otro medio (2 → 3). Es un proceso de presión constante, ya que la cámara está abierta para fluir hacia adentro y hacia afuera. El calor neto agregado viene dado por Q add = H 3 – H 2
- Expansión isentrópica : el aire calentado y presurizado se expande en la turbina y entrega su energía. El trabajo realizado por la turbina viene dado por W T = H 4 – H 3
- rechazo de calor isobárico : el calor residual debe rechazarse para cerrar el ciclo. El calor neto rechazado viene dado por Q re = H 4 – H 1
Como se puede ver, podemos describir y calcular (por ejemplo, eficiencia térmica ) tales ciclos (de manera similar para el ciclo de Rankine ) usando entalpías .
Ver también: Eficiencia térmica del ciclo de Brayton
Procesos isentrópicos en ciclos termodinámicos
Ciclo ideal de Carnot
- Compresión isentrópica
- Expansión isentrópica
Ciclo ideal de Rankine
- Compresión isentrópica en una bomba
- Expansión isentrópica en una turbina
Ciclo ideal de Brayton
- Compresión isentrópica en un compresor.
- Expansión isentrópica en una turbina
Ciclo ideal de Otto
- Compresión isentrópica
- Expansión isentrópica
Ciclo Diesel Ideal
- Compresión isentrópica
- Expansión isentrópica
Eficiencia isentrópica: turbina, compresor, boquilla
En capítulos anteriores supusimos que la expansión del gas es isentrópica y, por lo tanto, usamos T 4, es como la temperatura de salida del gas. Estos supuestos solo son aplicables con ciclos ideales.
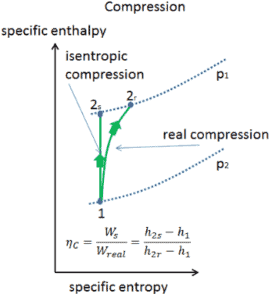
La mayoría de los dispositivos de flujo constante (turbinas, compresores, boquillas) funcionan en condiciones adiabáticas , pero no son realmente isentrópicos, sino que están idealizados como isentrópicos para fines de cálculo. Definimos los parámetros η T , η C , η N , como una relación entre el trabajo real realizado por el dispositivo y el trabajo del dispositivo cuando se opera en condiciones isentrópicas (en el caso de una turbina). Esta relación se conoce como la eficiencia de turbina isentrópica / compresor / boquilla .
Estos parámetros describen qué tan eficientemente una turbina, compresor o boquilla se aproxima a un dispositivo isentrópico correspondiente. Este parámetro reduce la eficiencia general y el rendimiento del trabajo. Para turbinas, el valor de η T es típicamente de 0.7 a 0.9 (70-90%).
Ejemplo: eficiencia de turbina isentrópica
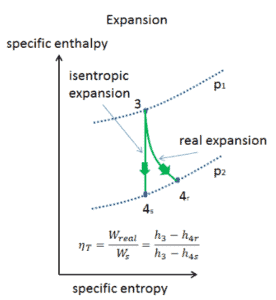
Suponga una expansión isentrópica de helio (3 → 4) en una turbina de gas. En estas turbinas, la etapa de alta presión recibe gas (punto 3 en la figura; p 3 = 6.7 MPa ; T 3 = 1190 K (917 ° C)) de un intercambiador de calor y lo expulsa a otro intercambiador de calor, donde la presión de salida es p 4 = 2.78 MPa (punto 4) . La temperatura (para el proceso isentrópico) del gas a la salida de la turbina es T 4s = 839 K (566 ° C).
Calcule el trabajo realizado por esta turbina y calcule la temperatura real a la salida de la turbina, cuando la eficiencia de la turbina isentrópica sea η T = 0.91 (91%) .
Solución:
A partir de la primera ley de la termodinámica, el trabajo realizado por la turbina en un proceso isentrópico se puede calcular a partir de:
W T = h 3 – h 4s → W Ts = c p (T 3 – T 4s )
Según la Ley del Gas Ideal, sabemos que el calor específico molar de un gas ideal monoatómico es:
C v = 3 / 2R = 12.5 J / mol K y C p = C v + R = 5 / 2R = 20.8 J / mol K
Transferimos las capacidades de calor específicas en unidades de J / kg K a través de:
c p = C p . 1 / M (peso molar de helio) = 20.8 x 4.10 -3 = 5200 J / kg K
El trabajo realizado por la turbina de gas en el proceso isentrópico es entonces:
W T, s = c p (T 3 – T 4s ) = 5200 x (1190 – 839) = 1.825 MJ / kg
El trabajo real realizado por la turbina de gas en el proceso adiabático es entonces:
W T, real = c p (T 3 – T 4s ). η T = 5200 x (1190 – 839) x 0.91 = 1.661 MJ / kg
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.