Cálculo del cabezal de la bomba – Cálculo del rendimiento de la bomba
 En este ejemplo, veremos cómo predecir
En este ejemplo, veremos cómo predecir
- la descarga de diseño
- potencia de agua
- la cabeza de la bomba
de una bomba centrífuga . Estos datos de rendimiento se derivarán de la ecuación de turbomáquina de Euler:
Par del eje: eje T = ρQ (r 2 V t2 – r 1 V t1 )
Potencia de agua: P w = ω. Eje T = ρQ (u 2 V t2 – u 1 V t1 )
Altura de la bomba: H = P w / ρgQ = (u 2 V t2 – u 1 V t1 ) / g
Se proporcionan los siguientes datos para una bomba de agua centrífuga:
- diámetros del impulsor en la entrada y salida
- r 1 = 10 cm
- r 2 = 20 cm
- Velocidad = 1500 rpm (revoluciones por minuto)
- el ángulo de la cuchilla en la entrada β 1 = 30 °
- el ángulo de la cuchilla en la salida β 2 = 20 °
- suponga que los anchos de la cuchilla en la entrada y en la salida son: b 1 = b 2 = 4 cm .
Solución:
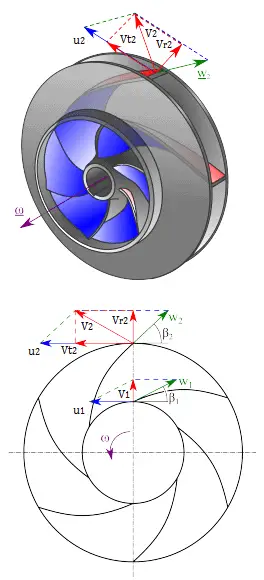
Primero, tenemos que calcular la velocidad radial del flujo en la salida. Desde el diagrama de velocidad, la velocidad radial es igual a (suponemos que el flujo entra exactamente normal al impulsor, por lo que el componente tangencial de la velocidad es cero):
V r1 = u 1 tan 30 ° = ω r 1 tan 30 ° = 2π x (1500/60) x 0.1 x tan 30 ° = 9.1 m / s
El componente radial de la velocidad del flujo determina cuánto ingresa el caudal en el impulsor . Entonces, cuando conocemos V r1 en la entrada, podemos determinar la descarga de esta bomba de acuerdo con la siguiente ecuación. Aquí b 1 significa el ancho de la pala del impulsor en la entrada.
Q = 2π.r 1 .b 1 .V r1 = 2n x 0,1 x 0,04 x 9,1 = 0,229 m 3 / s
Para calcular la potencia de agua (P w ) requerida, tenemos que determinar la velocidad de flujo tangencial de salida V t2 , porque se supone que la velocidad tangencial de entrada V t1 es igual a cero.
La velocidad de flujo radial de salida se deriva de la conservación de Q :
Q = 2π.r 2 .b 2 .V r2 ⇒ V r2 = Q / 2π.r 2 .b 2 = 0.229 / (2π x 0,2 x 0,04) = 4,56 m / s
A partir de la figura ( triángulo de velocidad ), el ángulo de salida de la cuchilla, β 2 , se puede representar fácilmente de la siguiente manera.
cot β 2 = (u 2 – V t2 ) / V r2
y, por lo tanto, la velocidad de flujo tangencial de salida V t2 es:
V t2 = u 2 – V r2 . cuna 20 ° = ω r 2 – V r2 . cuna 20 ° = 2π x 1500/60 x 0.2 – 4.56 x 2.75 = 31.4 – 12.5 = 18.9 m / s.
La potencia de agua requerida es entonces:
P w = ρ Q u 2 V t2 = 1000 [kg / m 3 ] x 0.229 [m 3 / s] x 31.4 [m / s] x 18.9 [m / s] = 135900 W = 135.6 kW
y la cabeza de la bomba es:
H ≈ P w / (ρ g Q) = 135900 / (1000 x 9.81 x 0.229) = 60.5 m
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.